Soalbagus.com - Soal Latihan Tes OSN ( Olimpiade Sains Nasional ) mata pelajaran Fisika untuk Tingkat Kabupaten atau Kota yang dilengkapi dengan kunci jawaban.
SOAL SELEKSI KOMPETISI SAINS TINGKAT KABUPATEN/KOTA 2020 CALON TIM KOMPETISI FISIKA INDONESIA 2021.
KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN SEKERTARIS JENDERAL KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN PUSAT PRESTASI NASIONAL TAHUN 2020
Soal tes seleksi OSN/ KSN Fisika ini terdiri dari 8 butir soal berupa essay dan diberikan waktu selama 180 menit untuk mengerjakannya. Berikut adalah soal-soalnya :
1. (8 poin) Sebuah benda A dapat bergerak tanpa gesekan sepanjang kawat berbentuk parabola yang memenuhi persamaan 𝑦 = 𝑎𝑥2 dengan a suatu konstanta positif, x adalah jarak horizontal dari sumbu simetri kawat, dan yadalah tinggi benda dari titik terendah kawat . Jika kawat ini diputar dengan kecepatan sudut 𝜔 dengan sumbu y sebagai porosnya, tentukan nilai 𝜔 (dinyatakan dalam 𝑔 dan 𝑎) agar benda A berada dalam keadaan setimbang!
2. (10 poin) Selama empat hari berturut-turut, seorang anak mulai berangkat dari rumah dengan berjalan kaki menuju sekolah selalu pada waktu keberangkatan yang sama. Bel masuk sekolah juga memang diset untuk berbunyi pada waktu yang selalu sama.
- Pada hari pertama, anak tersebut mulai berjalan dengan kecepatan awal 50 meter per menit dan dipercepat dengan percepatan 2 meter per menit2. Ternyata dia tiba di sekolah 5 menit setelah bel berbunyi.
- Pada hari kedua, anak tersebut mulai berjalan dengan kecepatan awal 150 meter per menit dan diperlambat dengan perlambatan 2 meter per menit2. Ternyata dia tiba di sekolah 5 menit sebelum bel berbunyi.
- Pada hari ketiga, ia memutuskan untuk berjalan dengan kecepatan konstan (yang nilainya lebih besar dari 100 meter per menit) hingga tiba di sekolah. Ternyata dia tiba di sekolah tepat saat bel berbunyi.
Jika pada hari keempat ia berjalan dengan kecepatan konstan 100 meter per menit, berapa menit ia tiba di sekolah setelah bel berbunyi ?.
3. (10 poin) Dua orang anak ingin melempar bola agar mengenai suatu sasaran di ujung tebing (titik Q). Mereka berdiri pada titik pelemparan (titik P) yang berada pada jarak tertentu dari sasaran. Mereka melempar bola dengan kelajuan awal yang sama pada waktu bersamaan, namun dengan sudut elevasi yang berbeda sehingga waktu yang ditempuh bola orang pertama dan kedua untuk mengenai sasaran masing-masing adalah 𝑡𝐴 dan 𝑡. Diketahui percepatan grativasi di tempat itu adalah 𝑔 . Tentukanlah jarak antara titik P dan titik Q (dinyatakan dalam 𝑡𝐴, dan 𝑡𝐵)!
4. (12 poin) Sebuah gunung dimodelkan sebagai kerucut dengan tinggi 𝐻 dan sudut setengah bukan 𝜃, dimana sin 𝜃 =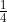 
. Sebuah lintasan yang mengitari gunung dibuat untuk menghubungkan titik 𝐴 pada dasar gunung dan titik 𝐵 pada permukaan gunung, dimana puncak gunung (titik 𝑃), titik 𝐴, dan titik 𝐵 terletak pada satu garis lurus. Panjang segmen garis lurus 
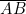adalah 
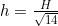. Lintasan dibuat menggunakan kawat dengan panjang minimum yang mengitari gunung. Sebuah partikel yang dapat bergerak bebas tanpa gesekan sepanjang lintasan kawat ditembakkan dari titik 𝐴 dan bergerak menuju titik 𝐵. Nyatakan semua jawaban dalam 𝐻 dan percepatan gravitasi 𝑔.
a. Tentukan kelajuan awal minimum partikel di titik 𝐴, yakni 𝑣, agar dapat mencapai titik 𝐵.
b. Jika partikel ditembakkan dari titik 𝐴 dengan kelajuan 𝑣 tersebut, hitung kelajuan partikel di titik 𝐵 yakni 𝑣′.
5. (15 poin) Dua benda bermassa 𝑚1 titik pelemparan dan 𝑚 2 (𝑚) berada segaris dan di atas bidang datar kasar dengan koefisien gesek statis dan kinetik bernilai sama yaitu 𝜇. Awalnya benda 1 berada di sebelah kiri benda 2, yang diam, sejauh L dan diberi kecepatan sebesar 𝑣1 ke kanan.
a. Tentukan syarat yang diperlukan agar benda pertama menumbuk benda kedua. Apabila syarat tersebut terpenuhi maka benda 1 akan menumbuk benda 2. Anggap tumbukan terjadi secara singkat sehingga bersifat lenting sempurna.
b. Tentukan dimanakah posisi akhir benda 1 dengan menganggap posisi tumbukan adalah pusat koordinat!
c. Tentukan dimanakah posisi akhir benda 2 dengan menganggap posisi tumbukan adalah pusat koordinat!
d. Berapakah jarak keduanya saat keduanya diam? Asumsikan volume kedua benda jauh lebih kecil dari jarak yang mereka tempuh.
6. (15 poin) Sebuah partikel bermassa 𝑚 meluncur di atas sebuah lengkungan logam licin ABC (titik B adalah titik terendah lintasan) yang berbentuk setengah lingkaran dengan jari -jari 𝑅 (lihat gambar). Selama partikel meluncur pada lengkungan, dua buah gaya
a. Usaha total oleh gaya
b. besar gaya kontak antara massa 𝑚 dengan lengkungan di titik B. Nyatakan jawaban Anda dalam 𝐹, 𝑅, 𝑚, 𝑔 dan 𝛽.
c. Besar gaya
Petunjuk: ∫ sin 𝑥 d𝑥 = − cos 𝑥 + 𝐶 dan ∫ cos 𝑥 d𝑥 = sin 𝑥 + 𝐶
7. (15 poin) Sebuah balok bermassa m1 berada di atas permukaan lantai yang licin. Pada balok terdapat tiang kokoh setinggi H yang massanya dapat diabaikan. Terdapat sistem bandul yang terdiri dari bola kecil bermassa m2 yang tergantung pada tali kokoh tak bermassa dengan panjang L (< H). Bandul tersebut dapat berayun bebas tanpa gesekan pada ujung atas tiang. Mula-mula posisi tali
sejajar dengan horisontal, kemudian seluruh sistem bergerak tanpa kecepatan awal. Percepatan gravitasi g ke bawah.
Tentukan:
a. tegangan tali sebagai fungsi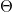
yaitu sudut antara tali dan tiang;
b. nilai tegangan tali maksimum serta kecepatan balok saat itu.
7. (15 poin) Sebuah balok bermassa m1 berada di atas permukaan lantai yang licin. Pada balok terdapat tiang kokoh setinggi H yang massanya dapat diabaikan. Terdapat sistem bandul yang terdiri dari bola kecil bermassa m2 yang tergantung pada tali kokoh tak bermassa dengan panjang L (< H). Bandul tersebut dapat berayun bebas tanpa gesekan pada ujung atas tiang. Mula-mula posisi tali
sejajar dengan horisontal, kemudian seluruh sistem bergerak tanpa kecepatan awal. Percepatan gravitasi g ke bawah.
Tentukan:
a. tegangan tali sebagai fungsi
b. nilai tegangan tali maksimum serta kecepatan balok saat itu.